-
Surprising Positive Semidefiniteness
They say that in Euclidean geometry, the solutions to all problems start by drawing a line somewhere in the picture. I think that this is characteristic of my favorite kind of proof, where you can’t just move forward in a linear fashion to get to an answer, but you actually have to add something new, that you might not have thought was related to the question.
Read more… -
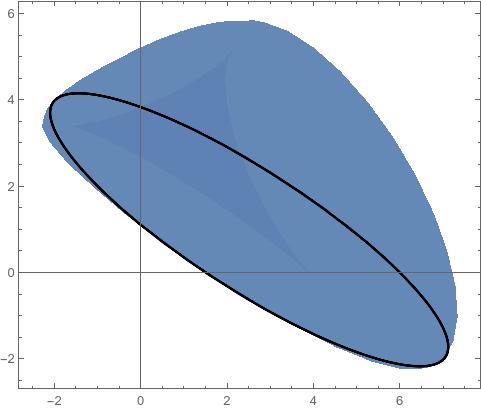
A Short Proof of Brickman's Theorem
This was based on a conversation with Alex Wang and Mark Gillespie. Alex has a blog post about Dine’s theorem, which is very related to this theorem. There are a lot of places in algebraic geometry where convexity appears in surprising places.
Read more… -
Inequalities between Binomial Coefficients in a Needlessly Fancy Way
Most high school students already know far more about the binomial coefficients than they need to, and one of the things that they might know is the fact that if $k < \frac{n}{2}$, then $$ \binom{n}{k} \le \binom{n}{k+1}.
Read more…